Хептагонални функции на призмата и как да изчислим обема
а седмоъгълна призма е геометрична фигура, която, както подсказва името, включва две геометрични дефиниции, които са: призма и хептагон.
"Призма" е геометрична фигура, ограничена от две бази, които са равни и паралелни полигони, а техните странични повърхности са успоредни..
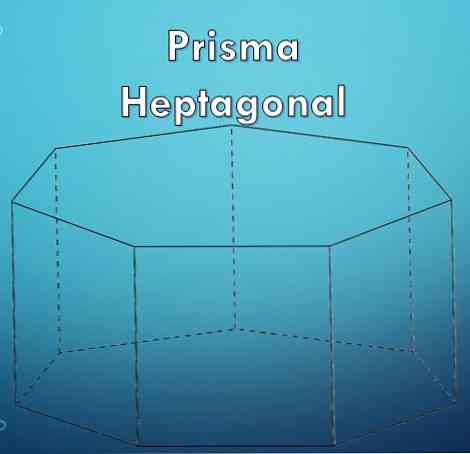
"Хептагон" е многоъгълник, който е оформен от седем (7) страни. Тъй като шестоъгълникът е многоъгълник, може да е, че той е редовен или неправилен.
Смята се, че полигонът е правилен, ако всичките му страни имат еднаква дължина и техните вътрешни ъгли измерват еднакво, те се наричат също и равностранени полигони; в противен случай се казва, че полигонът е неправилен.

Характеристики на седмоъгълна призма
Следват някои особености, които имат седмоъгълна призма, като: нейната конструкция, свойства на основите й, площта на всичките й лица и обема й.
1- Строителство
За изграждане на седмоъгълна призма са необходими два хептъна, които ще бъдат неговите основи и седем успоредника, по една от всяка страна на седмоъгълника.
Започнете, като изчертаете седмоъгълник, след това изтеглете седем вертикални линии с еднаква дължина, които идват от всеки от нейните върхове.
Накрая друг хептагон се начертава така, че върховете му да съвпадат с края на линиите, очертани в предишната стъпка.
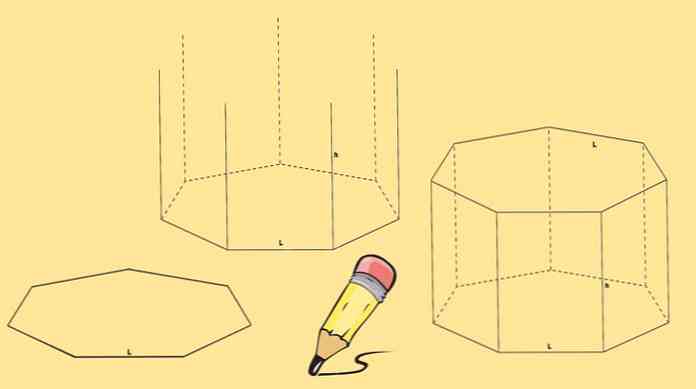
Хептагоналната призма, нарисувана по-горе, се нарича права хептагонална призма. Но също така можете да имате наклонена седмоъгълна призма, подобна на тази на следващата фигура.

2- Свойства на основите му
Тъй като техните бази са хептагони, те отговарят, че диагоналът е D = nx (n-3) / 2, където "n" е броят на страните на многоъгълника; в този случай имаме, че D = 7 × 4/2 = 14.
Можем също така да видим, че сумата от вътрешните ъгли на всеки хептагон (редовен или неправилен) е равна на 900º. Това може да бъде потвърдено от следното изображение.
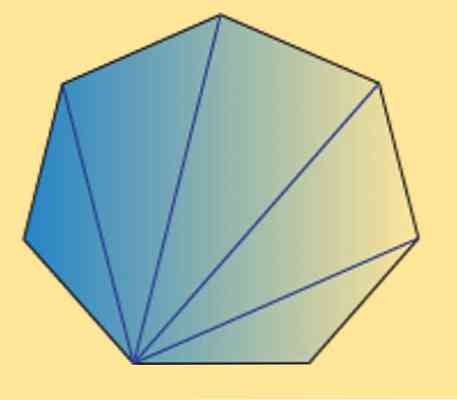
Както виждате, има 5 вътрешни триъгълника, и като се използва сумата от вътрешните ъгли на триъгълника е равна на 180º, може да се получи, че желания резултат.
3 - Зона, необходима за изграждане на седмоъгълна призма
Тъй като основите му са два хептагона и неговите страни са седем успоредни, площта, необходима за изграждане на седмоъгълна призма, е равна на 2xH + 7xP, където "H" е площта на всеки седмоъгълник и "P" площта на всеки паралелограма.
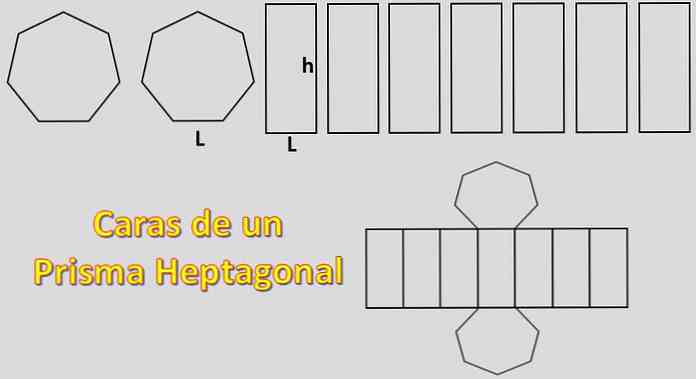
В този случай ще бъде изчислена площта на обикновения хептагон. За това е важно да се знае дефиницията на апотема.
Апотема е перпендикулярна линия, която преминава от центъра на правилния многоъгълник до средата на която и да е от неговите страни.
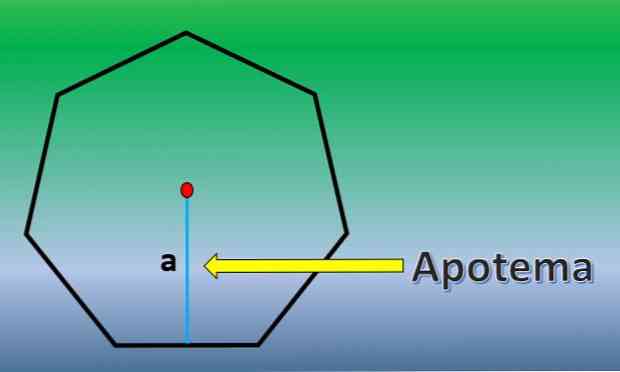
След като апотема е известен, площта на хептагона е H = 7xLxa / 2, където "L" е дължината на всяка страна и "а" дължината на апотема..
Площта на успоредника е лесна за изчисляване, дефинирана е като P = Lxh, където "L" е една и съща дължина на страната на седмоъгълника и "h" е височината на призмата.
В заключение, количеството материал, необходим за изграждане на хептугонална призма (с нормални бази) е 7xLxa + 7xLxh, т.е. 7xL (a + h).
4 - Обем
След като площта на основата и височината на призмата са известни, обемът се определя като (базова площ) x (височина).
В случая на хептагонална призма (с нормална основа) тя има, че нейният обем е V = 7xLxaxh / 2; може да се запише и като V = Pxaxh / 2, където "P" е периметърът на редовния хептагон.
препратки
- Billstein, R., Либескинд, С., & Lott, J. W. (2013). Математика: подход за решаване на проблеми за учителите в основното образование. López Mateos Editores.
- Fregoso, R. S., & Carrera, S.A. (2005). Математика 3. Редакция Progreso.
- Gallardo, G., & Pilar, P. M. (2005). Математика 6. Редакция Progreso.
- Gutiérrez, C.T., & Cisneros, M. P. (2005). Трети курс по математика. Редакция Progreso.
- Kinsey, L., & Moore, T.E. (2006). Симетрия, форма и пространство: Въведение в математиката чрез геометрия (илюстрирано, повторно отпечатване). Springer Science & Business Media.
- Mitchell, C. (1999). Ослепителен дизайн на математически линии (Илюстриран ред.). Scholastic Inc.
- R., M. P. (2005). Рисувам 6º. Редакция Progreso.


